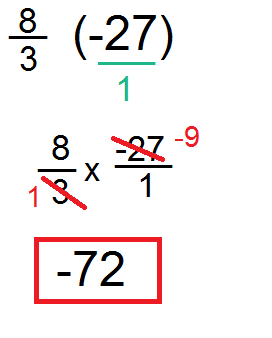Shane's Blog Post

Question 22

SAS= Side Angle Side rule

ASA= Angle Side Angle rule

SSA= Side Side Angle rule

HW:

Practise 3,5,6

Apply- all

Extend- any 3 of 13,14,15,16 and 17

*MANGAHIGH*

Cathlene's Blog Post

4.3 Similar Triangles

(Read page 146 to 149)

Proportional - in a shape it means same shape but different size

Corresponding - a comparison of two similar sides or angles in an object

Corresponding: LA ~ LD

LB ~ LE

LC ~ LF

LA = LBAC = LCAB LD = LEDF = LFDE

LB = LABC = LCBA LE = LDEF = LFED

LC = LACB = LBCA LF = LEFD = LDFE

Corresponding angles will ALWAYS be equal

The vertices are always upper case

Sides are always lower case

Example 2 ( Question 2 )

Homework

Check Your Understanding #1 and #2

Practise odds or even

Apply all question

Extend #18, #20, #22, #23

4.2 Scale

SCALE: is a comparison of two objects; the actual size and its diagram.

Scale can be expressed as a ratio, as a fraction, as a percent, in words or as a diagram.A scale of 1:50 means that 1 unit on the diagram is equal to 50 units of the actual object.

Scale Diagram: is similar o

r t

he actual or object. It main

There

are two ways to find a missing length of proportiontain proportion, the diagram may be longer or smaller than the actual object.

Example One: Use scale to determine the Actual Length of an Object.

For a scale of 1:14 and a

diagram measuring 5.5c

m set the proportion.

SCALE: is a comparison

of two objects; the actual size and its diagram.

Scale can be expressed as a ratio, as a fraction, as a percent, in words or as a diagram.

A scale of 1:50 means that 1 unit on the diagram is equal to 50 units of the actual object.

SCALE DIAGRAM :Is similar or the actual or

object. It maintain proportion, the diagram may

be longer or smaller than the actual object.

There are two ways to find a missing length of proportion

For a scale of 1:14 and a diagram measuring 5.5cm set the proportion.Example One: Use scale to determine the Actual Length of an Object.

Because it is easy to find the relationship of 1 to 5.5 it easy to find x, simply multiply 14 by 5.5 to find x=77cm- So the act

ual object is 77cm.

x= 5.5(14) x=77cm

Becau

se it is easy to find the relationship of 1 to 5.5 it easy to find x, simply multiply 14 by 5.5 to find x=77cm- So the actual object is 77cm.

Example Two: Use Measurement to find Scale.

So the scale is 1:2400000cm or 1:24km

Dont forget to do all the textbook work, worksheets and workbook work!!

And all mangahigh challenges are for marks! Keep playing! (:

Jocelyn's blog post on todays lesson

Today we learned about Enlargements and reductions.

Enlargement is to make something bigger. In mathematics we need to multiply by a factor greater than 1 to make it an enlargement. (eg. 3x2)

Reduction is to make something smaller. In mathematics we need to multiply by a factor that

is less than 1 but greater than 0 (eg. 7x0.2)

Scale Factor- the constant factor by which all dimensions of an object are to be inlarged or reduced. some examples of this is:

If a rectangle that is 3x5 is to be enlarged by a scale factor of 1.3 the new dimensions would be

3.9x6.5. If that same rectangle was to be Reduced by a scale factor of 0.6 the new dimensions would be 1.8x3

To make Enlargements and Reductions it must be proportional, maintaining its original shape, but not size.

Enlargements and Reductions can also be made on different sized graph paper. This method is often used by artistswhen drawing large murals from a small original, vice versa.

Homework:

Workbook 4.1

text 1,3

practise odd/even

apply 9,11,12,13

extend 14, 15, 17

extra practice worksheet

Lizelles text book question.

I'm truly sorry that this is late!!
My text book question is 27 on 2.4

"The surface area of a cube is 100 cm squared. Determine the edge length of the cube, to the nearest tenth of a centimetre."

A CUBE has 6 faces.

Since I knew that, I divided 100 cm squared by 6 to give me one face.
That got me 16.66 cm squared.
Since I wanted to get rid of the squared, I did a square root of a 16.66.
For that, I got 4.082.
I rounded that to the nearest tenth, and I got 4.1.

I checked at the book, and I got the same answer.



My question:





My work:

Jocelyn's textbook question 2.4

Question #19 in 2.4

A square picture with an area of 100cm^2 is mounted on matting 2.5 times the area of the picture. If the picture is centered on the matting, what is the width of the matting that is showing? Give your answer to the nearest tenth of a cm.

this is my work:

100x2.5=250

the square root of 100=10

the square root of 250=15.8113883

15.8113883-10=5.811388301

5.811388301/2=2.90569415

2.90569415=2.9

the width of the visible matting, to the nearest tenth of a cm. is, 2.9cm^2

Colleen's Blog Post

What we did in class today:















*You need to know the formula's for 3.4

Bacteria triples every 15 minutes.
Start with 50 bacteria.
The coefficient is 50.
50(3^1)
In one hour: 50(3^4)
In three hours: 50(3^12)
t hours: 50(3^4t)

Question from yesterday:


















Homework:
3.4- Show You Know
Check Your Understanding
Practice odd or even
Apply
Extend #13
Homework book
Extra Practice

Don't forget to do 3.3 if you're not done.
Don't forget to start your stash it.

Go on MANGAHIGH!

Jocelyn, it's your turn to do the blog.

Order of Operations

Today, in class we learned about order of operations..

the number in front of the power is called the coefficient.

the power is made up of the base-which is the 6

exponent- 2

The next question that we did worked on is..

use B.E.D.M.A.S.

Convert the next step into a fraction..

The next problems that we did were..

We have to find the exponent that equals the same as 81^4 and 8^3 with the base of 3 and 2.

Homework!!!

3.3

and GO ON MANGAHIGH!!!

And Colleen! I want you to do the next blog(: !!!!

Trisha's Blog Question

01. Calculate the dimensions of a square that has the same area as a circle with a radius of 5.7 cm. Round your answer to the nearest tenth of a centimetre.

A= √πr^2

A= √π5.7^2

A= √102.1

A= 10.1

The dimensions of a square that has the same area as a circle is 10.1 cm.

Jomer's Blog Post

In Class yesterday, Mr. Backe gave us some questions..

Another question he gave us..

The Faster Way

Product Law: When the bases are the same, simply add the two exponents to get the new power.

Product law means multiplying.

The faster way..

Another question..




Quotient Law: When the bases are the same, simply subtract the two exponents to get the new power.

Power of a power law: When a power is raised to a power simply multiply the two powers together to get the new product.

Another question



Another Question..








When a product is raised to an exponent, you can rewrite each number in the product with the same exponent.




Power of a quotient: When a quotient is raised to an exponent, you can rewrite each number in the quotient with the same exponent.

HOMEWORK!

Read pages 99-105.

Do SYK and CYU 1,2,3

Practise odd/even

Apply extend All

WorkBook 3.2

Extra Practise 3.1/3.2

Angelo's Blog Post

Powers & Exponent











Power of zero it will always be 1
any number or variable to an exponent of 1 is always itself
any exponent of 2 is always a perfect square and always an area
anything to an exponent of 3 represent perfect cube and represent volume









Homework
pg 92-95 3.1 Textbook and Homework book
Play Manga High
CYU 1,2,3
Practise 4-13
Apply Odd or Even
Extend 22 and 23

Lorriel's Textbook Question

Chapter 2.4 page 81

Question# 33

A square has an area of 32cm². What is the area of the largest circle that will fit inside it ? Express your answer to the nearest tenth of a square centimetre.

A= s²

√32cm= √s²

d= 5.7 r= 0.83

πr²= 8.949

2.83x2.83x3.14 = 25.1

Jieram's Textbook Question

Chapter 2.4 Page 79

Question 16 a)

The label on a 1-L can of paint states that the paint will cover an area of 10m^2. What is the side length of the largest square area that the paint will cover? Express you answer to the nearest hundredth of a metre.

To find the answer we have to get rid of the exponent. To do that square root 10.

I get..

but remember to round it to the nearest hundredth.

So I get 3.16

If you multiply 3.16 by 3.16 we get 9.98 or 10

The side length of the largest area that a 1-L can of paint can cover is 3.16

Cathlene's Textbook Question

Page 79 Question 24

b.

Robin's Textbook Question

2.4
Determining Square Roots of Rational Numbers




I Did C)
How i Did this is by




Then i did is





Then Get answer of


Then study for the MATH TEST TOMORROW!