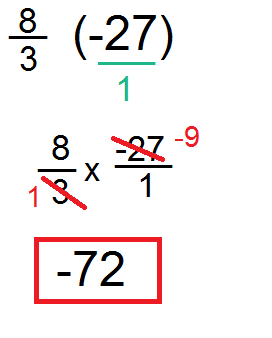Order of Operations

Today, in class we learned about order of operations..

the number in front of the power is called the coefficient.

the power is made up of the base-which is the 6

exponent- 2

The next question that we did worked on is..

use B.E.D.M.A.S.

Convert the next step into a fraction..

The next problems that we did were..

We have to find the exponent that equals the same as 81^4 and 8^3 with the base of 3 and 2.

Homework!!!

3.3

and GO ON MANGAHIGH!!!

And Colleen! I want you to do the next blog(: !!!!

Trisha's Blog Question

01. Calculate the dimensions of a square that has the same area as a circle with a radius of 5.7 cm. Round your answer to the nearest tenth of a centimetre.

A= √πr^2

A= √π5.7^2

A= √102.1

A= 10.1

The dimensions of a square that has the same area as a circle is 10.1 cm.

Jomer's Blog Post

In Class yesterday, Mr. Backe gave us some questions..

Another question he gave us..

The Faster Way

Product Law: When the bases are the same, simply add the two exponents to get the new power.

Product law means multiplying.

The faster way..

Another question..




Quotient Law: When the bases are the same, simply subtract the two exponents to get the new power.

Power of a power law: When a power is raised to a power simply multiply the two powers together to get the new product.

Another question



Another Question..








When a product is raised to an exponent, you can rewrite each number in the product with the same exponent.




Power of a quotient: When a quotient is raised to an exponent, you can rewrite each number in the quotient with the same exponent.

HOMEWORK!

Read pages 99-105.

Do SYK and CYU 1,2,3

Practise odd/even

Apply extend All

WorkBook 3.2

Extra Practise 3.1/3.2

Angelo's Blog Post

Powers & Exponent











Power of zero it will always be 1
any number or variable to an exponent of 1 is always itself
any exponent of 2 is always a perfect square and always an area
anything to an exponent of 3 represent perfect cube and represent volume









Homework
pg 92-95 3.1 Textbook and Homework book
Play Manga High
CYU 1,2,3
Practise 4-13
Apply Odd or Even
Extend 22 and 23

Lorriel's Textbook Question

Chapter 2.4 page 81

Question# 33

A square has an area of 32cm². What is the area of the largest circle that will fit inside it ? Express your answer to the nearest tenth of a square centimetre.

A= s²

√32cm= √s²

d= 5.7 r= 0.83

πr²= 8.949

2.83x2.83x3.14 = 25.1

Jieram's Textbook Question

Chapter 2.4 Page 79

Question 16 a)

The label on a 1-L can of paint states that the paint will cover an area of 10m^2. What is the side length of the largest square area that the paint will cover? Express you answer to the nearest hundredth of a metre.

To find the answer we have to get rid of the exponent. To do that square root 10.

I get..

but remember to round it to the nearest hundredth.

So I get 3.16

If you multiply 3.16 by 3.16 we get 9.98 or 10

The side length of the largest area that a 1-L can of paint can cover is 3.16

Cathlene's Textbook Question

Page 79 Question 24

b.

Robin's Textbook Question

2.4
Determining Square Roots of Rational Numbers




I Did C)
How i Did this is by




Then i did is





Then Get answer of


Then study for the MATH TEST TOMORROW!

Roemer's Blog Post

Glenn's Text Book Question

Chapter 2.4 Page 80.

Question 28 B)

The question is trying to say, find the answer for ....

(L) = 2.5

Once you figure out what "L" is you can start the math...

4 x 2.5 = 10

Then....

The answer will be 3.16

DON'T FORGET TO STUDY FOR THE MATH TEST, ALSO GO ON MANGAHIGH!!

Joshua's Textbook Question 2.4

#28 c)

So it takes 1.41s to complete a swing back and forth.

Jomer's Textbook work

Textbook page 79 #17b

17. Some parks contain fenced gardens. Suppose that it costs $80 to build each metre of fence, including materials and labour.

a) How much does it cost to enclose a square with an area of 120m²? express your answer to the nearest dollar.
$3504


B) Perdict whether the total cost of enclosing two squares with an area of 60m² each is the same as your answer to part a)


√60 = 7.75
7.75 x 4=31
31 x 80 = 2480
2480 x 2= $4960

The cost will not be the same.

Maya's Textbook Question

Question #22 on 2.4

The hypotenuse of an isosceles right triangle has a length of 20 cm. What is the length of each leg of the triangle? Provide your answer to the nearest tenth of a centimetre.


Each length of each leg of the triangle would be 14.1 cm.

Alec's Textbook Question

30. A square field has an area of 1000m^2. Laura wants to walk from one corner of the field to the opposite corner. If she walks at 1.5m/s, how much time can she save by walking diagonally instead of walking along two adjacent sides? Express your answer to the nearest tenth of a second.

First I want to get all the information we need in this question:

We need the time she walk diagonally and along adjacent sides

We need to the square root of 1000m^2

We need the hypotenuse

So lets figured out the hypotenuse of 1000m^2

Since we have a square, you only need to find 1 side because all sides are the same

Now I'm going to find the hypotenuse

Next I'm going to find how many seconds she walk along adjacent sides

Then I'm going to find how many seconds she's going to take to walk diagonally.

After having all that information I can figure out now the answer

Let x= time Laura spent walking along adjacent sides

Let y= time Laura spent walking diagonally.

X-Y= answer

It would look like this...

Chelsea's Textbook Question - 2.4

Here is the question from 2.4. I will be doing part A of it:

So it will cost $3504 to enclose a square with an area of 120m^2.

Olivia's Textbook Question 2.4

Question # 34 







Things to know:
- A = area
- r = radius
- π (pi) = 3.14159265...
- A of circular garden = 40 m²
- express answer to nearest tenth of a metre



First, you copy the formula from the question:

Next, fill in the values:
* it is not necessary to change π (pi)

Then, divide the area (A) of the circular garden by pi (π):
* use a calculator

Find the √12.73239545

Round 3.568248232 to the nearest tenth of a metre (m).

The answer is 3.6 m. 


Sorry about some of the pictures.